Dari sudut pandang geometri, nilai mutlak dari x ditulis | x |, adalah jarak dari x ke 0 pada garis bilangan real. Karena jarak selalu positif atau nol maka nilai mutlak x juga selalu bernilai positif atau nol untuk setiap x bilangan real.
Secara formal, nilai mutlak x didefinisikan dengan
atau dapat pula ditulis
| x | = -x jika x ≥ 0
| x | = -x jika x < 0
Dari Defenisi Tersebut dapat Disimpulkan Bahwa :
Nilai mutlak dari suatu bilangan merupakan jarak dari bilangan tersebut ke bilangan nol dan selalu bernilai positif.
Sebagai Contoh
| 7 | = 7
| 0 | = 0
| -4 | = -(-4) = 4
untuk Persamaan Nilai Mutlak Sendiri dapat Dinyatakan Dengan.
 |
Jadi, jelas bahwa nilai mutlak setiap bilangan real akan selalu bernilai positif atau nol.
Jika Persamaan tersebut kita kuadratkan dikedua ruas maka akan diperoleh suatu sifat nilai mutlak sebagai berikut.
Dari Persamaan inilah kita dapat menyelesaikan pertidaksamaan Nilai mutlak dengan menggunakan ketaksamaan segitiga pula yaitu (a + b ) (a - b).
|a| = a jika a > 0
= 0 jika a = 0
= -a jika a < 0
Sebagai contoh
|2| = 2 karena 2 > 0
|-2| = - (-2) = 2 Karena -2 < 0
|f(x)| = f(x) jika f(x) > 0
= 0 jika f(x) = 0
= - f(x) jika fx < 0
Contoh.
|2x - 3| = 2x - 3
karena 2x-3 > 0
maka 2x > 3
x > 3/2
| -(2x-3) | = -2x + 3
Karena -2x+3 < 0
maka -2x < -3
x < 3/2
Persamaan Nilai Mutlak
|f(x)| = a maka f(x) = a jika f(x) > 0
f(x) = 0 jika f(x) = 0
f(x) = -a jika fx < 0
Sebagai Contoh
|3x-7| =2 maka
3x - 7 = 2 jika 3x-7 > 0
3x = 2+7
x = 9/3
x = 3
3x - 7 = -2 jika 3x - 7 < 0
3x = -2+7
x = 5/3
Contoh soal
1. Tentukan nilai x yang memenuhi dari Persamaan |2x + 7| = 4.
Penyelesaian:
Positif Negatif
2x + 7 = 4 -(2x -7) = 4
2x = 4 – 7 -2x -7 = 4
x = -3/2 -7 – 4 = 2x
x = -11/2
Jadi penyelesaian dari |2x + 7| = 4 adalah x = -3/2 atau x = – 11/2.
2. Tentukan nilai x yang yang memenuhi persamaan |2x – 5| = 3 + 2 |7 – x|.
Penyelesaian:
|2x – 5| = 3 + 2 |7 – x| atau dapat ditulis |2x – 5| – 2|7 – x| = 3
Positif – Positif Negatif – Positif
(2x-5) – 2(7 – x) = 3 -(2x – 5) – 2(7 – x) = 3
2x + 2x = 3 +5 + 14 -2x+ 2x = 3 – 5 + 14
4x = 22 0x = 12
x = 11/2 Tidak ada bilangan real x yang memenuhi persamaan karena a = 0
Positif – Negatif Negatif – Positif
(2x – 5) – (-2)(7 – x) = 3 (2x – 5) – (- 2)(7 – x) = 3
(2x – 5) + 2(7 – x) = 3 (2x – 5) + 2(7 – x) = 3
2x -2x = 3 + 5 – 14 2x = 3 + 5 – 14
0x = 6 x = −3
Tidak ada bilangan real x yang memenuhi persamaan karena a = 0
Jadi penyelesaian dari |2x – 5| = 3 + 2 |7 – x| adalah x = 11/2 atau x = -3.
3. Tentukan nilai x yang yang memenuhi persamaan |3x – 5/3| = 1
Penyelesaian:
|3x – 5/3| = 1
Positif Negatif
3x -5/3 = 1 -(3x -5/3) = 1
3x = 1 + 5/3 -3x + 5/3 = 1
3x = 8/3 5/3 – 1 = 3x
x = 8/9 x = 2/9
Jadi penyelesaian dari |3x – 5/3| = 1 adalah x = 8/9 atau x = 2/9.
Untuk Penjelasan Lebih lengkap mengenai latihan soal bisa cek di video berikut
Kemudian Paparkan kesimpulan setiap orang dalam Group untuk didiskusikan bersama.

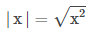

Tidak ada komentar:
Posting Komentar