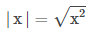Rabu, 30 Desember 2020
Model Pembelajran TGT ( Teams, Games and Tournament )
Minggu, 27 Desember 2020
Model Pembelajaran tipe NHT ( Number Head Together )
Jumat, 25 Desember 2020
Model Pembelajaran Jigsaw
Senin, 21 Desember 2020
Filsafat Pendidikan Matematika
Kumpulan Trik - Trik Matematika (Cara Cepat)
Bismillahirahmanirahim.
Kali ini admin membagikan beberapa trik atau cara cepat dalam menyelesaikan beberapa bentuk matematika nih.
Ada tingkat smp dan Sma.
Ayo mari dicek di video berikut
Sehingga bisa lebih mengerti trik-triknya.
1. Trik Penyelesaian Domain dan Range
3. Trik Penyelesaian Turunan
4. Trik penyelesaian barisan dan deret
5. Trik Penyelesaian SPLDV
Kamis, 17 Desember 2020
Filsafat Pendidikan Matematika
Minggu, 13 Desember 2020
RPP Model Pembelajaran NHT ( Number Head Together )
Filsafat Pendidikan Matematika
Kamis, 26 November 2020
KISI-KISI Lengkap Matematika Umum Ujian Akhir Semester Ganjil Kelas X
Rabu, 25 November 2020
Kumpulan Soal Semester Kelas X Part.2
Pertidaksamaan Rasional dan Irasional
1. Nilai x yang memenuhi (5x-1)/(x+2) ≥ 1 adalah…
2. pertidaksamaan (3x-7)/(x-1) ≤ 2 dipenuhi oleh…
3. pertidaksamaan √(6x-4 ) > √(2x+8) akan bernilai benar jika…
4. Nilai x yang memenuhi pertidaksamaan √(x^2-4 ) < √(x+2 ) adalah…
5. Himpunan penyelesaian dari pertidaksamaan x^2/(9- x^2 ) ≤ 0 adalah…
6. agar pecahan (x^2 + 3x – 10 )/(x^2-x+2) bernilai positif, maka x anggota himpunan…
7. Himpunan penyelesaian pertidaksamaan √(x^2-3x) < 2 adalah …
8. Tentukanlah himpunan penyelesaian dari pertidaksamaan rasional (x^2-3x-10)/(2x-3) ≥ 0
9. Tentukanlah himpunan penyelesaian dari pertidaksamaan Irasional √((x+9)/(4x-2)) > 1
Sistem Persamaan Linear Tiga Variabel
10. Enam tahun yang lalu umur citra 4 tahun lebih muda dari seperempat umur pak Bambang. Umur citra sekarang 3 tahun lebih tua dari seperdelapan umur pak Bambang Jumlah umur mereka adalah…
11. Tentukanlah nilai x, y dan z yang memenuhi dari persamaan liniear tiga variabel berikut!
i. x + 2y – 3z = - 4
ii. 2x – y + z = 3
iii. 3x + 2y + z = 10
12. Ati, Tia dan Ita pergi bersama-sama ke sebuah toko buah. Ati membeli 2 kg Apel, 2 Kg Anggur dan 1 Kg jeruk dengan harga Rp.67.000,-. Tia membeli 3 Kg Apel, 1 Kg Anggur, dan 1 Kg Jeruk dengan harga Rp. 61.000,-. Ita membeli 1 Kg Apel, 3 Kg anggur dan 2 Kg jeruk dengan harga Rp.80.000,-. Jika Wawan membeli 1 Kg apel, 1 Kg anggur dan 4 Kg jeruk ditoko yang sama dengan Ati, Tia dan Ita. Berapakah yang harus dibayar oleh Wawan.
13. Dalam suatu bazaar pakaian anak-anak pak Anton membayar Rp. 300.000,- untuk 2 baju dan 2 celana, sedangkan pak Firdaus membayar Rp. 675.000,- untuk 1 baju dan 6 celana. Jika x dan y berturut-turut menyatakan harga setiap baju dan celana, perbandingan nilai x dan y adalah…
14. Dua tahun yang lalu Seorang Ibu usianya 6 kali usia anaknya. Jika 18 tahun yang akan datang umur ibu tersebut 2 kali umur anaknya maka umur Ibu itu sekarang adalah.,.
15. Ani membeli 2 kg salak, 1 kg jeruk, dan 2 .kg mangga dengan harga Rp.70.000,-. Nisa membeli 2 kg salak, 2 kg jeruk, dan 1 kg mangga dengan harga Rp. 90.000,- Sementara itu Sani membeli 2 Kg salak, 3 Kg jeruk, dan 2 kg mangga dengan harga Rp. 130.000,- ditoko yang sama, jika sari akan membeli 3 kg salak dan 1 kg jeruk maka sari harus membayar dengan harga
16. Seorang saudagar mencampur 3 jenis teh. Apabila ia mengambil 15 kg teh jenis 1 dan 5 kg teh jenis 2, maka harga rata-ratanya adalah Rp.2.500.00, Apabila 25 kg teh jenis 1 dicampur dengan 15 kg teh jenis 3 maka harga rata-ratanya adalah Rp.2.630.00, jika 2 kg teh jenis 1 dicampur dengan 3 kg jenis ke 2 dan 5 kg teh jenis ke 3 maka harga rata-ratanya adalah Rp.2.750.00, Berapakah harga 1 kg tiap jenis teh tersebut.?
17. Sebuah bilangan terdiri atas tiga angka, yang jumlah angka-angkanya adalah 12. Apabila bilangan yang terbentuk oleh kedua angka yang pertama dibagi dengan angka terakhir, maka hasil baginya adalah 4, dan apabila angka puluhan dibagi jumlah dari kedua angka lainya, maka hasil baginya ½ . Bilangan berapakah bilangan tersebut.
18. Pada suatu perusahaan mebel, kemampuan dan keterampilan pekerjanya rata-rata sana. Untuk merakit 6 set kursi selama 12 hari dibutuhkan tenaga 8 orang. Jika ingin merakit 50 set kursi dengan 32 orang pekerja, maka waktu yang diperluhkan adalah
19. Sebuah bilangan terdiri atas tiga angka. Apabila bilangan tersebut dibagi dengan bilangan yang diperoleh dari urutan terbalik ketiga angka tersebut, maka hasilnya sama dengan 2 dan sisanya adalah 25. Angka puluhan kurang satu dari dua kali jumlah ratusan dan satuan. Apabila angka satuan dikurangkan dengan angka puluhan, maka hasilnya adalah dua kali bilangan ratusan. Tentukan bilangan itu
20. Ani dan Dian bekerja bersama-sama dapat menyeleikan sebuah pekerjaan selama 4 hari. Dian dan Toto bekerja bersama-sama dapat menyelesaikan pekerjaan yang sama selama 3 hari, sedangkan Ani dan Toto bekerja bersama-sama dapat menyelesaikan pekerjaan tersebut selama 2,4 hari. Jika mereka bekerja sendiri-sendiri, maka berapakah waktu yang mereka butuhkan.?
Selasa, 24 November 2020
Cara Memasukkan File (Word, Exel, PDF, PPT ) Ke Bloggspot
Berikut adalah salah satu cara memasang (embed) dokumen berbentuk Word, Excel, PPT dan PDF pada blog atau website kita melalui google docs. Google docs merupakan media penyimpanan berbagai dokumen kita yang dapat dilihat secara langsung secara online tanpa mendownloadnya terlebih dahulu. Bagi anda yang baru pertama kali masuk ke google docs, maka anda harus setuju dengan peraturan yang di buat oleh google. Berikut adalah cara embed/ pasang dokumen google drive pada blog atau website.
Langkah 1 : upload file ke google docs.
1. Silahkan login ke https://drive.google.com/
dengan account gmail anda.
2. Klik tab BARU
3. Klik tombol UPLOAD
4. Masukan file yang ingin anda upload (word, excel, power point).
5. Klik tombol Upload File yang ada di sebelah bawahnya.
6. Tunggu beberapa saat sampai file anda terupload semuanya (tergantung dari besarnya file serta kecepatan koneksi anda).
7. Jika sudah terupload, anda bisa mengeditnya jika mau yaitu dengan mengeklik dokumen yang telah terupload.
8. Kemudian pilih bagikan
9. Maka muncul menu sharing settings.
10. Copy link to share ke notepad atau text editor lainnya.
11. Kemudian klik Selesai
15. Yang kita butuhkan bukanlah semua kode yang sudah kita copy sebelumnya (perhatikan kode yang berwarna Biru, ini adalah kode yang kita butuhkan)
https://docs.google.com/document/d/1KzgroUVft146VRZAZweRSTrI8_JNE9BTvjV4F6cpY4w/edit
maka yang kita copy cukup kode tersebut ( 1KzgroUVft146VRZAZweRSTrI8_JNE9BTvjV4F6cpY4w)
16. Terakhir, paste kode di bawah ini pada postingan blog dengan mengganti “(paste disini)” termasuk tanda kurung "()"]dengan kode yang sudah kita dapat sebelumnya, (untuk ukuran bisa disesuaikan sendiri)
<iframe src="https://docs.google.com/viewer?srcid=(paste disini)&pid=explorer&chrome=false&embedded=true" width="500" height="600"></iframe>
17. Selesai.
Langkah 2 : posting kode google docs ke blogger.
1. Silahkan login ke blogger dengan ID anda.
2. Klik Posting Baru.
3. Silahkan anda buat postingan yang anda inginkan.
4. Ketika anda mau menyisipkan kode yang dari google docs, klik terlebih dahulu tab Edit HTML ( jangan yang compose)
5. Paste kode google docs yang ada di notepad tadi pada tempat yang anda inginkan.
6. Klik Tombol MEMPUBLIKASIKAN POSTING.
7. Silahkan lihat hasilnya.
8. Selesai.
Minggu, 22 November 2020
Persamaan dan Pertidaksamaan Nilai Mutlak
Dari sudut pandang geometri, nilai mutlak dari x ditulis | x |, adalah jarak dari x ke 0 pada garis bilangan real. Karena jarak selalu positif atau nol maka nilai mutlak x juga selalu bernilai positif atau nol untuk setiap x bilangan real.
Secara formal, nilai mutlak x didefinisikan dengan
atau dapat pula ditulis
| x | = -x jika x ≥ 0
| x | = -x jika x < 0
Dari Defenisi Tersebut dapat Disimpulkan Bahwa :
Nilai mutlak dari suatu bilangan merupakan jarak dari bilangan tersebut ke bilangan nol dan selalu bernilai positif.
Sebagai Contoh
| 7 | = 7
| 0 | = 0
| -4 | = -(-4) = 4
untuk Persamaan Nilai Mutlak Sendiri dapat Dinyatakan Dengan.
 |
Jadi, jelas bahwa nilai mutlak setiap bilangan real akan selalu bernilai positif atau nol.
Minggu, 15 November 2020
Komposisi Transformasi
Komposisi Transformasi.
1. Dua Translasi berurutan.
Jika suatu titik mendapatkan translasi T1, kemudian dilanjutkan dengan translasi T2, maka dua translasi tersebut dapat dinyatakan dengan transformasi tunggal dan ditulis dengan notasi "T2 o T1".
Dibawah ini ditunjukkan titik p (x,y) mendapat transformasi berurutan.
T1 = (a b) dan T2= ( c d)
Maka titik P (x,y) ====>T1 diperoleh p' = (x+a, y+b)
Kemudian
Titik P' ( x+a, y+b) =====> T2 diperoleh p" = (x + a + c, y + b + d)
Jika kita perhatikan T2 o T1 yang memetakan titik P' ke titik P", maka pemetaaan tersebut dapat kita nyatakan sebagai berikut.
Titik P ( x,y) =======> T2 o T1 diperoleh P" = [x + (a+c) , y + ( b + d)] sehingga
Dapat dinyatakan rumus untuk komposisi transformasi T2 o T1 adalah.
T2 o T1 = ( a+c, b+d)
Contoh;
Tentukanlah bayangan titik (3,2) oleh translasi T1 = ( 5 2) dan dilanjutkan oleh translasi T2 = ( 1 3)
Jawaban.
T2 o T1 = (5+1 2+3)
= ( 6 5)
Maka
Titik ( 3 , 2 ) ===> T2 o T1 diperoleh
(3+6, 2+5) = ( 9, 7)
Sehingga diperoleh bayangaan titik (3, 2) oleh translasi T1 dilanjutkan T2 adalah (9,7)
Untuk mengigat kembali materi translasi.
Silahkan dicek kembali videonya.
Rabu, 11 November 2020
Kumpulan Soal Matematika Kelas X Semester Ganjil
Nilai Mutlak.
- Tentukanlah nilai x yang memenuhi persamaan nilai mutlak berikut.
- |(3x-5)/4x-7| = 5
- |2x-9|= x-3
- |x-1|² - |2x-2| - 3 = 0
- Buatkanlah sifat-sifat persamaan nilai mutlak
- |(X-6)/3x-9| ≤ 2
- |(2x - 9)/6 |≥ x
- |x-1|² - |x+3| - 2 < 0
- Sifat-sifat dari Pertidaksamaan Nilai Mutlak
- Nilai x yang memenuhi (2x - 1) / ( 3x - 5) ≥ 1 adalah…
- Himpunan penyelesaian dari pertidaksamaan rasional 2x / (x-1)² ≥ 4/x adalah…
- Tentukanlah sifat-sifat dari penyesaian pertidaksamaan rasional dan Irasional
- Tentukanlah himpunan penyelesaian dari pertidaksamaan Irasional √ [(x-3)/(2x - 1) ]> 1
- Himpunan penyelesaian dari √ ( x² - 2x +1) < 4 adalah...
Selasa, 10 November 2020
Dilatasi dan Rotasi
Pengertian Dilatasi
Dilatasi merupakan transformasi geometri berupa perkalian yang memperbesar atau memperkecil suatu bangunan geometri. Dalam konsep dilatasi, ada yang disebut titik dilatasi dan faktor dilatasi. Titik dilatasi merupakan titik yang menentukan posisi suatu dilatasi.
Pengertian Rotasi
Rotasi adalah perputaran benda pada suatu sumbu yang tetap, misalnya perputaran gasing dan perputaran bumi pada poros/sumbunya.
Untuk Penjelasan Lebih Lengkap, perhatikan penjelasan dari video berikut.
Minggu, 08 November 2020
Refleksi (Pencerminan)
Transformasi Geometri
Setelah sebelumnya kita telah membahas translasi atau pergeseran sekarang kita akan membahas.
Refleksi Atau Pencermian
Seperti halnya bayangan benda yang terbentuk dari sebuah cermin. Sebuah objek yang mengalami refleksi akan memiliki bayangan benda yang dihasilkan oleh sebuah cermin. Hasil dari refleksi dalam bidang kartesius tergantung sumbu yang menjadi cerminnya. Pembahasan materi refleksi yang akan diberikan ada tujuh jenis. Jenis-jenis tersebut antara lain adalah refleksi terhadap sumbu x, sumbu y, garis y = x, garis y = -x, titik O (0,0), garis x = h, dan garis y = k. Berikut ini adalah ringkasan daftar matriks transformasi pada refleksi/pencerminan.
Pencerminan terhadap sumbu x
Pada pencerminan terhadap sumbu x, nilai absis tetap dan ordinat menjadi kebalikannya.
Pencerminan Terhadap Sumbu y
Pencerminan terhadap sumbu y, merupakan kebalikan dari pencerminan terhadap sumbu x. Di mana nilai absis menjadi kebalikannya dan nilai ordinatnya tetap.
Pencerminan terhadap Garis y = x
Pada pencerminan terhadap garis y = x akan mengakibatkan nilai absis menjadi ordinat. Begitu juga, nilai ordinat akan menjadi absis.
Pencerminan terhadap Garis y = – x
Pencerminan terhadap garis y = – x akan membuat nilai absis menjadi kebalikan dari ordinat. Sedangkan nilai ordinat akan menjadi kebalikan dari absis.
Pencerminan terhadap Titik Asal O(0,0)
Pencerminan pada titik asal artinya melakukan pencerminan terhadap titik O (0,0). Hasil pencerminan terhadap titik asal adalah nilai absis dan ordinat menjadi kebalikannya.
Pencerminan terhadap Garis x = h
Pencerminan terhadap garis x = h akan membuat titik absis bergeser sejauh 2h. Sedangkan nilai titik ordinatnya tetap.
Pencerminan terhadap Garis y = k
Pencerminan terhadap garis y = k akan membuat titik ordinatnya bergeser sejauh 2k. Sedangkan nilai titik absisnya tetap.
Kumpulan Soal Fungsi Kuadrat
- Persamaan sumbu simetri parabola y = 8 - 2x - x² adalah.
- Koordinat titik balik grafik fungsi dengan rumus f(x) = 3 - 2x - x² adalah.
- Sebuah roket ditembakkan vertikal keatas mencapai tinggi h meter setelah x detik dirumuskan dengan rumus h(t) = 400t-5t² tinggi maksimum roket tersebut adalah.
- Grafik fungsi kuadrat yang persamaannya y = ax² - 8x + 6, memotong sumbu x, satu diantara titik potongnya adalah (3,0), maka nilai a adalah.
Fungsi Kuadrat
A. Pengertian Fungsi Kuadrat
Defenisi fungsi dapat ditinjau dari 2 hal berikut.
- Fungsi sebagai Pemetaan
- Fungsi sebagai pasangan berurut
- Fungsi kuadrata dinytakan dengan y = ax² + bx +c atau f(x) = ax² + bx + c dengan a ≠ 0; a, b, c elemen bilangan Real, x disebut variabel bebas dan y disebut variabel terikat
- Diskriminan D = b² - 4ac
- Grafik fungsi kuadrat pada umumnya sdlalu berbentuk parabola baik itu terbuka keatas maupun terbuka kebawah.
- Kurva akan memotong sumbo x untuk y = 0
- Kurva akan memotong sumbu y untuk x = 0 dengan titik potong pada (0,c)
- Mempunyai sumbu simetri x = -b/2a
- Bentuk umum fungsi Kuadrat dapat ditulisakan sebagai berikut y = ax² + bx +c atau f(x) = ax² + bx + c dengan a ≠ 0; a, b, c elemen bilangan Real
- Dengan a menunjukkan kurva terbuka keatas atau kebawah. Jika a > 0 maka kurva terbuka keatas dan mencapai puncak minimum, dan jika a < 0 maka kurva terbuka ke bawah dan mencapai puncak maksimum.
- Titik puncak = titik ekstrim = titik balik = titik stationer yang biasa disimbol (x indeks e, y indeks e), dengan Xe , Ye = ( -b/2a, -D/4a )
- Xe = Sumbu Simetri dan Ye = nilai balik/nilai ekstrim/nilai stationer
Sabtu, 07 November 2020
Pemanfaatan tringonometri dalam kehidupan
Selasa, 03 November 2020
Translasi.
Tranlasi.
Merupakan suatu sub bab pada materi transformasi geometri.
Translasi artinya pergeseran, sehingga translasi merupakan pergeseran suatu objek yang berupa titik, garis, bangun, dimensi dua maupun dimensi 3, translasi disimbolkan dengan Translasi T.
Sebagai contoh.
Translasi T = ( a b) yang artinya benda atau titik digeser kearah a (kiri jika a < 0 atau kanan jika a > 0 ) dan disgeser ke arah b ( ke bawah jika b < 0 atau ke atas jika b > 0), jika a dan b = 0 artinya benda tersebut tetap.
1. Translasi Titik pada titik.
Jika diberikan suatu titik A yaitu ( 4, 3) dan ditranslasikan T = ( - 2 7) artinya adalah titik A tersebut digeser kearah kiri sejauh dua satuan dan digeser kearah atas sejauh 7 satuan maka titik yang diperoleh setelah digeser ialah A' = ( 2, 10)
Atau dapat dirumuskan dengan
Jika suatu titik A = ( x, y) dan ditranslasikan terhadap T = (a , b ) maka bayangan atau A' = ( x + a, y + b )
2. Translasi garis pada suatu titik.
Jika diberikan suatu gari yang melalui titik-titik tertentu maka kita bisa mencari menggunakan cara translasi titik pada titik.
Namun jika diberikan suatu persamaan maka kita bisa menggunakan dua cara.
Cara 1 yaitu mencari dengan menggunakan translasi titiik pada suatu titik
Cara 2 yaitu dengan menggunakan persamaan bayangan pada matriks tersebut yaitu dengan menggunakan rumus x' = x + h, y' = y + k kemudian menggunakan rumus y - y1 = m ( x - x1 )
Sebagai contoh.
Jika suatu persamaan gari y = 2x - 3 ditranslasikan terhadap T = ( 0 2 ) maka dapat diselesaikan dengan cara.
Cara 1.
Dengan mencari titik sembarang pada persamaan garis y = 2x - 3
Dengan mengambil sembarang titik.
Jika x = 0 maka y = 2.0 - 3 = - 3 sehingga titik yang diperoleh adalah A = ( 0, -3)
Jika x = 1 maka y = 2. 1 - 3 = -1 sehingga titik yang diperoleh adalah B = (1,-1)
Jdi sekarang kita translasikan titik tersebut pada translasi T = ( 0 2)
A' = ( 0+0 , -3 + 2 ) = (0, -1 )
B' = ( 1 + 0 , -1 + 2 ) = ( 1, 1)
Setelah itu kita tinggal menguhubungkan titik tersebut untuk mendapatkan garis tersebut.
Jika ditanyakan persamaan garis tersebut.
Tinggal menggunakan rumus persamaan yang melalui dua titik yaitu (y - y1)/(y2- y1) = (x - x1) / (x2 - x1)
Untuk lebih jelasnya cek penjelasan video berikut.
Jumat, 30 Oktober 2020
Rumus keliling dan Luas Bangun Datar
Rumus keliling dan Luas Bangun Datar
Rumus PersegiKeliling : 4 x Sisi
contoh : Sisi = 5 cm
Keliling = 4 x 5
= 20 cm
Luas : Sisi x Sisi
contoh : Sisi = 5 cm
Luas = 5 x 5
= 25 cm2
Keliling : 2 x (Panjang + Lebar)
Keliling persegi panjang = 2 x panjang + 2 x lebar
contoh : Panjang = 6 cm
Lebar = 4 cm
Keliling = 2 x (6 + 4) = 20 cm
keliling = 2 x 6 + 2 x 4 = 12 + 8 = 20 cm
Luas : Panjang x Lebar
contoh : Panjang = 8 cm
lebar = 5 cm
Luas = 8 x 5
= 40 cm2
Contoh : AB = 8 cm
AC = 10 cm
BC = 6 cm
Kelililng : 8 + 10 + 6
= 24 cm
Luas Segitiga : 1/2 x alas (BC) x tinggi AB
1/2 x 6 x 8
= 24 cm2
Rumus Lingkaran
Kamis, 29 Oktober 2020
Banyak Faktor Positif dan Jumlah Faktor Positif.
Faktor
Merupakan kumpulan bilangan yang dapat membagi habis suatu bilangan dengan bilangan lainya.
contoh Faktor dari 12 terdiri atas ( 1, 2, 3, 4, 6, 12)
Faktor Prima
Merupakan kumpulan bilangan prima yang dapat membagi habis suatu bilangan dengan bilangan lainya.
contoh faktor Prima dari 12 yaitu ( 2, 2 , 3 ) atau bisa dituliskan 2^2 . 3
Faktor Positif
Merupakan faktor atau bilangan yang habis membagi suatu bilangan dimana faktor-faktornya merupakan suatu bilangan positif.
Sebagai contoh Faktor dari 12 terdiri atas ( 1, 2, 3, 4, 6, 12)
sehingga bisa dikatakan banyak Faktor positifnya sebanyak 6 yaitu ( 1, 2, 3, 4, 6, 12 )
Dan Jumlah faktor Positifnya yaitu 1 + 2 + 3 + 4 + 6 + 12 = 28
Namun bagaimana jika bilangan bulatnya cukup besar?
apakah kalian angka mencarinya secara manual ?
tentunya akan membutuhkan waktu yang cukup lama yah.
oleh karena itu berikut cara mudah untuk mencari banyak faktor Positif dan jumlah faktor Positif.
Jika suatu bilangan cacah memiliki faktor Prima a^m . b ^n . c^o . . . .
- maka dapat dinyatakan banyak faktor Positif dari bilangan tersebut adalah
( m + 1 ) * ( n + 1) * ( o + 1 ) . . .
- maka jumlah faktor positif dari bilangan tersebut dapat dinyakan dengan